No matter how many figures aspirate to the iron throne of geometry but triangles will always rule the world like Jon Snow.

Triangles come in different shapes and different sizes and we impose them a name for each of the types: equilateral, isosceles, rectangle, etc. But they are a more powerful tool than a description given by merely a word.
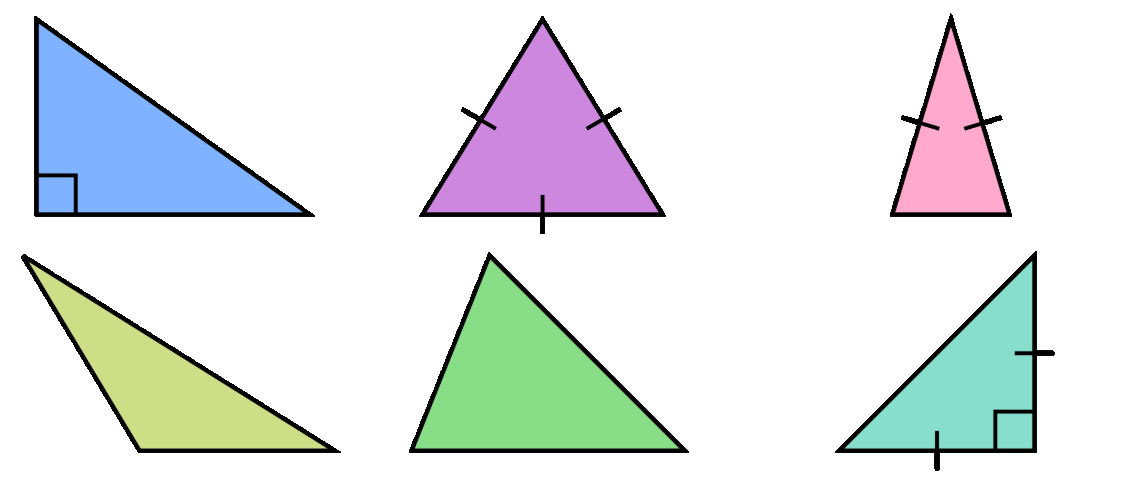
I normally work with points, 3D points. Sometimes half a million 3D points and I need to connect them. I can connect them in triangles and quadrangles, and ever quadrangles are much easier to define. Triangles are 90% of the times the best choice. Since most of the times, I start with quadrangles, I end up splitting them into triangles.
- QUADS: They ensure a clean topology and makes the model deform properly when animated.
- TRIS: They tend to give problems when you try to increase the resolution of the model downsampling it.
So why I prefer triangles?
Cos I’m a trouble’ make’. Just kidding.
They are cheap, fast, and accurate. They are the easiest primitive to define a closed area and also to define a plane. They are the rendering superstars and of course, they are always convex area. Changing the direction of the normal is as easy as change the order of the vertices from clockwise to counterclockwise so what else do you need to know to love triangles?

How did I take advantage of triangles in my last paper?
The paper I presented at International Conference on Pattern Recognition 2018 was called 2D-to-3D Facial Expression Transfer but don’t let it lie to you, it could be named I’m f***ing in love with triangles, but editors wouldn’t accept it. You can find all the information about this paper (the formal and boring one) here.
Triangles are a good way to define sub-regions in space and use as clusters since there are a lot of techniques that can be useful for this task, like ray tracing.
If we have a face, with 68 landmarks, we can easily define 101 dalmatians regions between them and we will have a beautiful makeup artwork worthy of David Bowie.

If we assign each of the points to the most likely region on several faces, we will have them grouped in semantic equivalent regions. A little step further, if the parametrize the points with respect to the evolving triangle in barycentric coordinates, we can deform the vertices of the triangle to adapt other shapes and the points will lie in an equivalent relation with their connection points. It’s like a David Copperfield trick, but it’s all about Math. (Now tell me if you don’t love triangles).
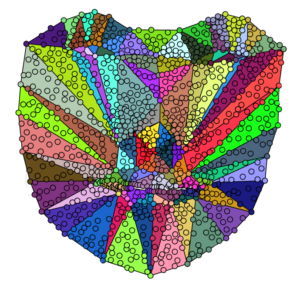
And then we can go one step further to assign all the points of a face with the most plausible triangular element of the same semantic region. So we can have a one to one correspondence with meshes at different resolution!

But why do we need a one-to-one correspondence?
One-to-one correspondence means direct and easy operation. Means invertibility, reciprocity, and all that good things. If we have a one to one correspondence everything happening in one of the sides can be easily defined or transferred on the other side. If we have a one-to-triangle correspondence, don’t panic, is also a good thing. We just need to transfer the effect of the transformation of the vertices to the point using its barycentric coordinates.

In our case, once we have a one-to-triangle correspondence we can operate from a mesh to the other one with the mapping functions defined in the paper, and transfer expressions from a face to another one with different resolution, geometry even topology changes in an easy manner.

If you want a deeper detail on my work, please visit the paper page, and don’t hesitate to contact me!

This time the song is old, it’s from an Australian indie band called … The TRIANGLES. Enjoy! (the images are from my lovely island)

After I realized that I never would be winning an Olympic gold in the 200m butterfly, I spend many years thinking about what to do in life, researching which path should I follow to accomplish my life goals that were on reach. So, it’s not surprising that after many efforts in this research I became a researcher. First a news researcher (or call it journalist if you prefer) and later a scientific researcher.


Hi,
I am a computer science student on my last year at Florida State University, I’m very interested in 3D geometry and I wonder if you could send me the code of your work because I’m very interested in this topic and of course if we can keep contact for future collaborations.
Cheers!
Joe
Hey Joe! I’m glad you are visiting me and showing your interest in my work. The code is something I have in my short-term to-do list. But for sure I’ll let you know when I release it openly. Hope I’ll have a nice last year at univ 🙂
I am really impressed with your writing skills and also with the layout on your weblog. Is this a paid theme or did you modify it yourself? Anyway keep up the excellent quality writing, it抯 rare to see a nice blog like this one nowadays..
I do agree with all of the ideas you have presented in your post. They are very convincing and will definitely work. Still, the posts are very short for novices. Could you please extend them a bit from next time? Thanks for the post.
nice article, waiting for your another 🙂